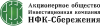Портфельная теория Марковица: основы и пример подсчета доходности
Любые вложения денег сопровождаются рисками. Их степень определяется конечным доходом. Если он высокий, то риски тоже высокие. Инвесторы и трейдеры рынка ценных бумаг мечтают добиться максимальной доходности при минимальных рисках. Соотношению этих двух параметров уделяется много внимания.
Выдающиеся математики-экономисты пытаются найти «золотую середину». Но их расчеты приводят лишь к выявлению определенных догм. Например, выбор подходящего времени для размещения свободных средств (покупки активов) не имеет ключевого значения. Почти 90% дохода зависит от оптимального распределения денег.
Игроки фондового рынка создают портфели и покупают разные ценные бумаги. Они вкладывают в многочисленные активы, тем самым уменьшая риск потери всего капитала. Этот принцип подробно описан в десятках портфельных теорий. Все они основаны на научной работе известного экономиста Гарри Марковица.
Содержание:
- Краткая история
- Насколько важно диверсифицировать портфель?
- Эффективная граница — что это такое?
- На каких формулах и расчетах строится метод Марковица?
- Пример подсчета ожидаемой доходности по формуле Марковица в Excel
- Преимущества метода Марковица
- Недостатки теории
- Дополнения теории Марковица
- Заключение
Краткая история

В 1950-1951 годах Марковиц работал над докторской диссертацией по экономике. В процессе написания научного труда у него появилась идея диверсификации (распределения) капитала при инвестировании. Она легла в основу будущей портфельной теории Марковица.
В 1952-м году была опубликована статья скромного аспиранта в «Финансовом журнале». Называлась она – «Выбор портфеля». В ней Гарри предложил математический способ формирования портфеля.
Он обозначил определенные условия рынка, при которых его методы позволят построить оптимальный портфель (с максимальной доходностью и минимальными рисками). В него должны входить активы, которые между собой слабо коррелируют (практически не имеют взаимной связи).
Главная заслуга аспиранта заключалась в следующем – он предложил перевести процесс выбора инвестиционного портфеля в плоскость формальной математики. Обозначил прямую связь между понятиями риска и доходности.
Следующие 7 лет экономист занимался развитием и усовершенствованием своей теории. В 1959-м году он опубликовал монографию. В ней были описаны основные положения статьи, размещенной в 1952-м году в «Финансовом журнале». В 1990-м Марковиц был удостоен Нобелевской премии за теорию портфельных инвестиций.
Удивительно, но этот человек получил признание только спустя 40 лет после своего экономического открытия. Многие связывают это с тем, что только в начале девяностых появились компьютеры. С их помощью удалось оценить эффективность математического (вероятностного) подхода к формированию оптимального портфеля.
Насколько важно диверсифицировать портфель?

Диверсификация подразумевает включение разных видов активов в инвестиционный портфель. Такой подход помогает выстроить оптимальную структуру ценных бумаг. Способствует снижению уровня финансовых рисков. Позволяет увеличить доход в краткосрочной и долгосрочной перспективе.
За счет распределения свободных средств удается избежать серьезной финансовой просадки в момент падения стоимости определенных активов, входящих в портфель. Например, цена акций компании начала падать. По этому активу инвестор ушел в минус, но смог компенсировать убытки благодаря росту стоимости акций других компаний.
Эксперты считают, что диверсифицированным можно считать портфель, в котором собрано от 8-ми до 20-ти финансовых инструментов (активов). Например:
- ценные бумаги;
- ПИФ-ы;
- драгоценные металлы;
- объекты недвижимости;
- ETF индексы.
Как видите, диверсификация является важнейшим этапом в формировании оптимального портфеля. Модель Марковица опирается именно на нее.
Эффективная граница — что это такое?
При формировании портфеля инвестору (трейдеру) нужно определить пропорцию разных активов (долю каждого вида финансового инструмента). Предположим, что у него 100% облигаций в портфеле. Если он добавит акции, то доходность возрастёт вместе с рисками. Чем больше доля акций в портфеле, тем выше риски. Но как найти «золотую середину»? С помощью эффективной границы.
Это набор портфелей с оптимальными пропорциями активов, которые позволят получить максимальную прибыль при минимально возможных рисках. Нет портфелей, которые имели такое соотношение дохода-риска, которое бы выводило их выше эффективной границы. Но зато существуют те, которые находятся ниже ее (они либо чересчур рискованные, либо не приносят ожидаемый уровень прибыли).
На каких формулах и расчетах строится метод Марковица? Он рассчитан на решение двух главных задач – достигнуть предельной доходности при заданном уровне риска и добиться минимальных рисков при низком пределе доходности. Строится метод на следующих формулах:
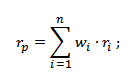
где: rp – это ожидаемая доходность сформированного портфеля, wi – доля конкретного актива, ri – доходность актива за определенный период, n- количество разных активов. Получается, что ожидаемая доходность всего портфеля зависит от суммы доходностей каждого актива, входящего в него.
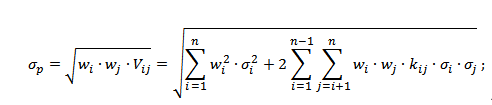
где: σp – это риск всего портфеля, σi – стандартный показатель отклонения уровня доходности i-актива, kij – коэффициент соотношения (корреляции) двух активов (i,j), wi – доля i-актива в портфеле, Vij – совместное изменение доходности двух активов (ковариация), n – количество активов, входящих в портфель инвестора.
Пример подсчета ожидаемой доходности по формуле Марковица в Excel
Согласно рассматриваемой теории, оптимальным считается портфель, в котором собраны разные группы активов. Например, облигации, фьючерсы, акции, индексы, опционы. Диверсификация минимизирует риски и позволяет выявить отрицательные взаимные соотношения (корреляции). Для лучшего понимания вышеописанных формул проведем простые расчеты.
Дано: портфель с акциями американских компаний, представляющих разные сегменты рынка – Visa, Macys, AT&T, Apple.
- Действие первое – необходимо выгрузить в Excel котировки акций этих компаний за весь прошлый год. Действие второе – нужно посчитать доходность каждого актива. Имеется в виду изменения его стоимости на протяжении 12-ти месяцев. Дивиденды тут не учитываются.
- Цены активов выгружены в виде таблицы. Напротив каждой строки с месяцем есть строка со стоимостью. Необходимо определить доходность по каждому месяцу с помощью формулы натурального логарифма в Эксель.Например, в июне 2021 года цена акции Visa была равна 200 рублей, а в июле она составила 205 рублей. Нужно второй значение разделить на первое – получится 2,5%. Это доходность за июль. Аналогичным образом нужно посчитать по другим месяцам. Это касается и активов других компаний.
- Далее нужно высчитать среднее значение доходности за год. Прибавьте все проценты доходности за каждый месяц и разделите на 12. Выполните эту процедуру относительно каждого актива, входящего в портфель. К примеру, ожидаемый доход акций компании AT&T оказался отрицательным. Нужно убрать этот актив из портфеля.
- Теперь необходимо определить уровень риска каждой акции, используя функционал Excel. Для этого следует воспользоваться формулой стандартного отклонения. Выберите ее в меню Эксель и выделите столбец с ценами актива за год. Система сама посчитает уровень риска.
- Следующий шаг – расчет ковариации акций, собранных в портфель. В Excel есть специальная надстройка, которая поможет нам на этом этапе. Нужно открыть вкладку «Данные» и выбрать пункт «Анализ данных» и найти в предложенном списке команду «Ковариация». Откроется окно, в котором следует указать ячейки с ежемесячными ценами определенного актива и выбрать группировку по столбцам.
- После определения ожидаемой доходности каждой акции, можно переходить к расчету ожидаемой доходности всего портфеля, который состоит из этих активов. Для этого необходимо определить доли акций трех американских компаний, собранных в портфеле. Напомним, что активы четвертой компании мы убрал, так как у них отрицательная доходность за год.
Допустим, что доля акций Visa в портфеле составляет 25%, акций Macys – 25%, Apple – 50%. Нужно определить средневзвешенный показатель доходности акции каждой компании. Формула простая:
(Ожидаемая доходность Visa * ковариация Visa) + (Ожидаемая доходность Macys * ковариация Macys) + (Ожидаемая доходность Apple * ковариация Apple). - Теперь необходимо определить общий риск портфеля. В Экселе есть формула массива – КОРЕНЬ (МУМНОЖ(МУМНОЖ(доля Visa в портфеле : доля Apple; ковариация Visa : ковариация Apple); доля Visa : доля Apple)).
Пример оптимизации портфеля
Рей Далио разработал стратегию всепогодного портфеля. Она одна из самых надежных и известных. На ее принципах были построены фонды OPNW и TRUR. Классический всепогодный портфель легко воссоздается за счет пяти индексных фондов (ETF) – GLD (с портфельной долей 7,5%), DBC (с долей 7,5%), IEF (15%), TLT (40%), VTI (30%).
Чтобы понять наглядно суть стратегии Рея Далио, нужно подробно изучить всепогодный портфель. В частности, его изменения за последние десять лет, без учета инфляции.
| Название ETF | Показатель доходности | Предельная просадка | Корреляция с индексом S&P 500 | Коэффициент Уильяма Шарпа |
| VTI | 13,37% | −20,84% | 1 | 0,92 |
| TLT | 8,32% | −18,03% | −0,42 | 0,64 |
| IEF | 4,54% | −7,6% | −0,4 | 0,73 |
| DBC | −6,37% | −64,83% | 0,57 | −0,34 |
| GLD | 1,87% | −42,91% | 0,08 | 0,16 |
Самый слабый фонд DBC. Размер ежегодного убытка по нему составил 6,37%, а взаимозависимость с бенчмарком (показатель с образцовой доходностью) составила 0,57. Такая корреляция чересчур большая. У других диверсификаторов нет такого значения.
Нужно модифицировать всепогодный портфель, убрав DBC и добавив XLU. Этот фонд выбран по причине более привлекательных показателей. Итог оптимизации всепогодного портфеля: GLD (с портфельной долей 7,5%), XLU (с долей 7,5%), IEF (15%), TLT (30%), VTI (40%).
Преимущества метода Марковица
Эта модель позволяет применить систематизированный подход к составлению инвестиционного портфеля. На основании несложных математических формул и опцией Excel можно высчитать оптимальную пропорцию активов. Другие плюсы метода:
- он не сложный для понимания (начинающий инвестор/трейдер быстро разберётся во всех нюансах);
- подходит для разных видов активов – индексы, фьючерсы, облигации, недвижимость, деривативы, акции, опционы;
- позволяет определить не единственный оптимальный вариант формирования портфеля, а множество вариантов, которые помогут заработать максимально много при минимальных рисках;
- обеспечивает стабильность и структурированность активов;
- избавляет от высоких рисков – финансовые инструменты, собранные в портфеле по методу Марковица не могут быть задействованы в спекуляциях.
Модель 1959 года остается актуальной и по сегодняшний день. Правда в оригинальном виде она уже не применяется. Ее совершенствовали и приспособили к современным реалиям.
Недостатки теории
Теория портфелей, предложенная Гарри Марковицем, имеет свои минусы. О некоторых из них вы уже наверно догадались при изучении процесса расчета ожидаемой доходности акций американских компаний. Итак, недостатки теории:
- Она рассчитана для рынка, на котором постоянно растут котировки финансовых инструментов и отсутствуют ощутимые колебания курса. Подобные процессы характерны для экономики прошлых лет. Сегодня рынок более неустойчив в этом плане. Следовательно, показатель корреляции активов регулярно меняется. Это не уменьшает уровень рисков портфеля.
- Модель Марковица определяет потенциальную прибыль с активов, как среднеарифметическое значение. Учитываются только исторические котировки финансовых инструментов. При этом не берутся во внимание многочисленные макроэкономические факторы – инфляция, изменение отраслевых цен, уровень ВВП страны и др. А также микроэкономические факторы – рентабельность, бизнес-деятельность компании, ликвидность акций.
- Риски определяются исходя из степени изменения доходности по отношению к среднеарифметическому значению.
Последователи Марковица смогли решить многие недостатки его теории. Ими стали опытные экономисты – Сортино, Трейнор, Швагер, Модильяни и Шарп.
Дополнения теории Марковица
Экономист Уильям Шарп ввел такие понятия, как несистематический и систематический риск. Первый распространяется на отдельно взятый актив, а второй – на весь рынок. Также он предложил более эффективную альтернативу процессу вычисления корреляции финансовых инструментов, входящих в портфель. Суть предложения – считать взаимозависимость для одного конкретного актива и для рынка.
На практике для объективной оценки рынка ценных бумаг применяются специальные индексы. А взаимосвязь определяется методом расчета Бета-коэффициента. Что это такое? Отношение ковариации доходности всего рынка/одного актива к стандартному рыночному отклонению (значение возводится в квадрат). Подобное нововведение существенно упростило процесс расчета риска и дохода портфеля.
Бета-коэффициент – это показатель, обозначающий направление/амплитуду движения актива по отношению к широкому рынку. Под последним понимают значение, определяющее текущее состояние экономики страны. Например, индекс S&P500 покрывает 80% всей капитализации рынка США. По нему можно понять текущее положение дел в экономике этого государства.
На этом Уильям Шарп не остановился. Он смог понять, как нужно сравнивать портфели, у которых разные показатели доходности и риска. Значение, полученное путем такого сравнения, он назвал коэффициентом Шарпа. Чем выше коэффициент, тем выгоднее инвестиционный портфель.

Джек Трейнор также внес свою лепту в совершенство теории Марковица. Он предложил убрать из формулы Гарри значение риска портфеля и использовать вместо него Бета-коэффициент. Суть изменения – инвестор может справиться с несистематическим риском путем дополнительной диверсификации, поэтому следует учитывать в расчетах только систематические риски (то есть, Бета-коэффициент).

Ф. Сортино предложил брать во внимание исключительно падение котировок активов. При этом стандартные отклонения инвестиционных убытков должны заменить общее отклонение. Ввел в расчет собственный коэффициент. Он определяет причины сверхнормативной доходности – был принят излишний риск при подсчетах или была применена профессиональная инвестиционная идея.
Заключение
Портфельные инвестиции – это самый популярный и финансово выгодный формат вложения свободных денег в активы. Задача трейдера/инвестора сводится к правильному выбору финансовых инструментов. Также ему нужно выстроить правильную структуру портфеля. Это поможет минимизировать риски и увеличить доходность.
Для формирования структуры портфеля нужно воспользоваться формулами Марковица, которые были усовершенствованы современными экономистами. Весь процесс расчетов можно осуществлять в Excel. Эту процедуру нужно повторять с определённой периодичностью, так как рынок изменчив. Главное, владеть входными данными и правильно понимать полученные результаты подсчетов.